머신러닝 - 2930 Blog

**서포트 벡터 머신(Support Vector Machine, SVM)**은 머신러닝의 대표적인 지도학습 알고리즘으로, 분류(Classification)와 회귀(Regression) 문제를 해결하는 데 널리 사용됩니다. 특히 고차원 데이터에서도 뛰어난 성능을 보이며, **마진 최대화(Maximum Margin)**라는 독특한 학습 방식을 통해 높은 정확도와 안정성을 제공합니다.

1. SVM의 기본 개념

1.1 SVM이란?

SVM은 **데이터 포인트를 기반으로 최적의 결정 경계(Decision Boundary)**를 찾아내는 알고리즘입니다. 이때, 각 클래스 사이의 **마진(Margin, 여백)**을 최대화하는 **초평면(Hyperplane)**을 학습합니다.

마진: 각 클래스와 초평면 사이의 거리.
초평면: 데이터를 분리하는 N차원 공간의 선(2D), 평면(3D), 또는 고차원의 경계.

SVM의 목표는 이 마진을 최대화하여 새로운 데이터가 들어왔을 때 정확하게 분류할 수 있도록 하는 것입니다.

1.2 주요 개념 설명

용어	설명
서포트 벡터(Support Vector)	마진 경계에 가장 가까이 위치한 데이터 포인트. SVM은 이 서포트 벡터에 의해 결정됩니다.
마진(Margin)	초평면과 각 클래스 사이의 최소 거리. 마진이 클수록 일반화 성능이 높아집니다.
초평면(Hyperplane)	데이터를 나누는 결정 경계. N차원 공간에서 w⋅x+b=0w \cdot x + b = 0w⋅x+b=0으로 표현.
커널 함수(Kernel)	비선형 데이터를 고차원으로 변환하여 선형 분리가 가능하게 하는 함수.

2. SVM의 작동 원리

2.1 마진 최대화

SVM은 다음과 같은 **최적화 문제(Optimization Problem)**를 풀어 마진을 최대화합니다:

최소화:

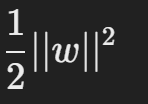
제약조건:

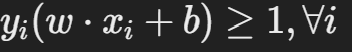
여기서,

www는 초평면의 가중치 벡터,
x_i는 데이터 포인트,
y_i는 클래스 라벨(+1 또는 -1),
b는 바이어스 항입니다.

2.2 선형 SVM과 비선형 SVM

선형 SVM: 데이터가 선형적으로 구분될 때 사용.
비선형 SVM: 데이터가 선형적으로 구분되지 않을 때 **커널 함수(Kernel Trick)**를 사용하여 고차원 공간에서 선형 분리가 가능하게 변환.

3. 커널 함수(Kernel Trick)

비선형 데이터를 처리하기 위해 SVM은 커널 함수를 사용하여 저차원의 데이터를 고차원 공간으로 변환합니다.

커널 함수	설명
선형 커널	K(x,y)=x⋅y
다항 커널(Polynomial)	K(x,y)=(x⋅y+1)^d
가우시안 RBF 커널	( K(x, y) = \exp(-\gamma
시그모이드 커널	K(x,y)=tanh⁡(αx⋅y+c)

가우시안 RBF 커널은 가장 널리 사용되는 커널로, 데이터의 거리에 따라 유사도를 측정합니다.

4. SVM의 장단점

4.1 장점

고차원 데이터에서도 성능이 뛰어남: 차원의 저주(Curse of Dimensionality)를 효과적으로 처리.
마진 최대화로 일반화 성능 우수: 오버피팅(Overfitting) 가능성이 낮음.
커널 함수 사용으로 비선형 문제도 해결: 복잡한 데이터 구조에도 적합.

4.2 단점

대규모 데이터셋에서는 학습 속도가 느림: 학습 시간이 오래 걸리고, 메모리 사용량이 많음.
하이퍼파라미터 튜닝 필요: 커널, CCC(규제 항), γ\gammaγ(RBF 커널 파라미터) 등 튜닝이 복잡.
해석이 어려움: 결과가 ‘블랙박스’처럼 느껴질 수 있음.

5. SVM의 활용 분야

5.1 이미지 분류

손글씨 인식(MNIST), 얼굴 인식, 의료 영상 분석 등 이미지 데이터의 분류에 활용.
**HOG(Histogram of Oriented Gradients)**와 같은 특징 추출 기법과 함께 사용.

5.2 텍스트 분류

스팸 메일 필터링, 감정 분석, 주제 분류 등 텍스트 데이터의 분류에 효과적.
TF-IDF와 같은 텍스트 벡터화 기법과 결합하여 사용.

5.3 바이오인포매틱스

DNA, RNA, 단백질 서열 분석 등 생명과학 분야의 데이터 분석.
유전자 발현 데이터 분류에 활용.

5.4 금융 및 리스크 분석

신용평가, 사기 탐지, 주식 가격 움직임 예측 등 금융 데이터 분석.
고차원 금융 데이터를 다룰 때 유리함.

6. SVM Python 구현 (Scikit-Learn 활용)

6.1 데이터 준비

<python>

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

# Iris 데이터셋 로드
data = load_iris()
X = data.data
y = data.target

# 데이터 분할 (80% 학습, 20% 테스트)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

6.2 SVM 모델 학습

<python>

from sklearn.svm import SVC

# SVM 모델 생성 (RBF 커널 사용)
model = SVC(kernel='rbf', C=1.0, gamma='scale')

# 모델 학습
model.fit(X_train, y_train)

6.3 예측 및 평가

<python>

from sklearn.metrics import accuracy_score, confusion_matrix

# 예측
y_pred = model.predict(X_test)

# 정확도 평가
print("Accuracy:", accuracy_score(y_test, y_pred))

# 혼동 행렬 출력
print("Confusion Matrix:\n", confusion_matrix(y_test, y_pred))

6.4 하이퍼파라미터 튜닝 (GridSearchCV 활용)

<python>

from sklearn.model_selection import GridSearchCV

# 하이퍼파라미터 후보 설정
param_grid = {
    'C': [0.1, 1, 10, 100],
    'gamma': ['scale', 0.01, 0.1, 1],
    'kernel': ['rbf', 'poly', 'linear']
}

# GridSearchCV 수행
grid_search = GridSearchCV(SVC(), param_grid, cv=5)
grid_search.fit(X_train, y_train)

print("Best parameters:", grid_search.best_params_)

7. SVM 성능 최적화 팁

데이터 스케일링: StandardScaler나 MinMaxScaler로 입력 데이터를 표준화.
커널 함수 선택: 선형 데이터는 linear, 비선형 데이터는 rbf 추천.
하이퍼파라미터 튜닝: C(규제 항)를 키우면 복잡한 모델(오버피팅), 줄이면 단순한 모델(언더피팅).
특징 선택: 너무 많은 특징은 학습을 어렵게 하므로, 중요한 특징만 선택.

8. 결론

SVM은 복잡한 고차원 데이터에서도 뛰어난 성능을 발휘하는 강력한 머신러닝 알고리즘입니다. 마진 최대화와 커널 트릭을 통해 선형/비선형 분류 문제를 효과적으로 해결할 수 있으며, 이미지 분류, 텍스트 분석, 금융 데이터 분석 등 다양한 분야에서 활발히 사용되고 있습니다.

미래에는 SVM이 딥러닝과 결합되어 더욱 강력한 하이브리드 모델로 발전할 가능성도 있으며, 양자 컴퓨팅 기반 SVM 등 새로운 기술과 융합되어 데이터 분석의 새로운 지평을 열어갈 것입니다. 🚀

[태그:] 머신러닝

서포트 벡터 머신(Support Vector Machine, SVM): 강력한 분류와 회귀 분석 알고리즘