마르코프 결정 과정(Markov Decision Process, MDP): 강화학습의 수학적 기초

1. 마르코프 결정 과정(MDP)란?

마르코프 결정 과정(Markov Decision Process, MDP)은 확률적 환경에서 최적의 의사결정을 내리기 위한 수학적 모델입니다. 이는 강화학습(Reinforcement Learning, RL)의 기초가 되는 핵심 개념으로, 다양한 AI 시스템이 환경과 상호작용하면서 학습하는 방식의 수학적 기반을 제공합니다.

MDP는 에이전트(Agent)가 환경(Environment)에서 상태(State)를 기반으로 행동(Action)을 선택하고, 그에 대한 보상(Reward)을 받으며 학습하는 과정을 수학적으로 모델링합니다.

2. MDP의 기본 구성 요소

MDP는 다음과 같은 5가지 요소로 구성됩니다.

2.1 상태 (State, S)

  • 환경의 현재 상태를 나타내는 변수.
  • 예: 자율주행차의 현재 위치, 바둑판의 상태, 게임에서의 캐릭터 위치.

2.2 행동 (Action, A)

  • 특정 상태에서 수행할 수 있는 선택지.
  • 예: 자동차가 이동할 방향(좌/우/직진), 게임에서 점프/공격/이동.

2.3 상태 전이 확률 (Transition Probability, P)

  • 특정 상태에서 특정 행동을 수행했을 때, 다른 상태로 전이될 확률.
  • P(s’ | s, a): 현재 상태(s)에서 행동(a)을 했을 때, 다음 상태(s’)로 전이될 확률.
  • 예: 바둑에서 돌을 두었을 때 다음 가능한 보드 상태.

2.4 보상 (Reward, R)

  • 특정 상태에서 특정 행동을 했을 때 얻는 보상.
  • 예: 게임에서 적을 물리쳤을 때 점수를 얻음, 자율주행차가 목적지에 도착하면 +100 보상.

2.5 정책 (Policy, π)

  • 주어진 상태에서 어떤 행동을 선택할지 결정하는 전략.
  • π(a | s): 특정 상태(s)에서 특정 행동(a)을 선택할 확률.
  • 최적의 정책을 찾는 것이 MDP의 목표.

3. 마르코프 속성 (Markov Property)

MDP는 마르코프 속성을 만족해야 합니다.

  • 현재 상태 StS_tSt​만 알고 있으면, 미래 상태 St+1S_{t+1}St+1​를 예측할 수 있음.
  • 즉, 과거의 상태들은 현재 상태에 포함되므로, 과거 정보를 추가로 고려할 필요 없음.

수식적으로:P(St+1∣St,At)=P(St+1∣S1,S2,…,St,At)

즉, 현재 상태만 알면 미래 상태를 예측할 수 있으며, 과거 정보는 필요 없음.

이러한 특성 덕분에, MDP는 복잡한 시스템을 단순하게 모델링하는 데 유용합니다.

4. MDP의 작동 방식

MDP는 에이전트가 환경과 상호작용하면서 최적의 정책을 학습하는 과정을 나타냅니다.

  1. 에이전트가 현재 상태 St를 관찰.
  2. 정책 π에 따라 행동 At​를 선택.
  3. 행동 At를 수행한 결과, 새로운 상태 St+1로 전이.
  4. 보상 Rt를 받음.
  5. 이 과정을 반복하면서 최적의 정책을 학습.

5. 강화학습에서 MDP의 활용

MDP는 강화학습에서 최적의 정책을 찾는 문제를 공식화하는 핵심 도구입니다. 강화학습에서 에이전트는 최대 보상을 얻을 수 있는 정책을 학습하며, 이를 위해 다음과 같은 알고리즘을 활용합니다.

5.1 가치 함수 (Value Function)

  • 특정 상태에서 장기적으로 받을 수 있는 기대 보상을 나타내는 함수.
  • 상태 가치 함수 (State Value Function, V(s):

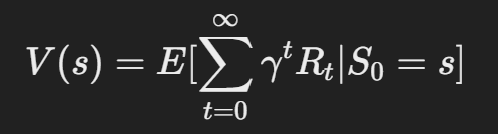
  • 현재 상태 s에서 시작했을 때, 미래에 받을 총 보상의 기댓값.
  • 행동 가치 함수 (Action Value Function, Q(s,a)):
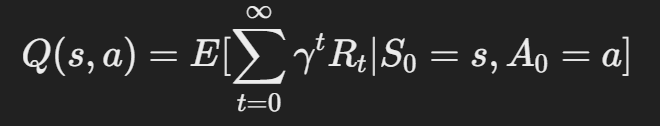
  • 특정 상태 sss에서 특정 행동 aaa를 했을 때 기대되는 보상.

5.2 최적 정책 찾기

  • **벨만 방정식 (Bellman Equation)**을 활용하여 최적 정책을 찾음.
  • 벨만 방정식:
  • 여기서 γ는 할인율(Discount Factor)이며, 미래 보상의 중요도를 결정.

5.3 대표적인 강화학습 알고리즘

  1. Q-Learning: Q-테이블을 이용하여 최적 정책 학습.
  2. Deep Q-Network(DQN): Q-Learning을 딥러닝으로 확장한 방법.
  3. Policy Gradient: 정책을 직접 최적화하는 방법.
  4. Actor-Critic: 정책 기반과 가치 기반 방법을 결합.

6. 마르코프 결정 과정(MDP) 예제

6.1 예제 1: 단순한 게임

가상의 게임에서 MDP를 적용해 보겠습니다.

  • 상태 SSS: 캐릭터의 현재 위치 (예: 왼쪽, 가운데, 오른쪽).
  • 행동 AAA: 좌, 우 이동.
  • 보상 RRR:
    • 목표 지점 도착 시 +10.
    • 잘못된 방향으로 이동 시 -1.
  • 상태 전이 확률 PPP:
    • 특정 확률로 다른 위치로 이동.

MDP를 적용하면, 최적의 정책은 “최소한의 움직임으로 목표 지점에 도달하는 것”이 됩니다.

7. 마르코프 결정 과정의 실제 활용

MDP는 다양한 산업에서 활용됩니다.

7.1 로보틱스

  • 로봇이 환경과 상호작용하며 최적의 경로를 학습.

7.2 금융 및 투자

  • 주식 시장에서 최적의 매매 전략을 결정하는 데 사용.

7.3 헬스케어

  • 치료 최적화: 환자의 건강 상태에 따라 최적의 치료 방법을 결정.

7.4 자율 주행

  • 차량이 현재 상태를 기반으로 최적의 주행 경로를 선택.

8. 결론

마르코프 결정 과정(MDP)은 강화학습의 핵심 이론적 기반으로, 다양한 AI 시스템에서 최적의 의사결정을 내리는 데 사용됩니다. MDP를 활용하면, 불확실한 환경에서도 최적의 행동을 학습하는 모델을 설계할 수 있습니다.

앞으로 강화학습과 MDP 기반 기술은 자율주행, 금융, 로보틱스 등 다양한 분야에서 더욱 중요해질 것이며, 이를 이해하고 활용하는 능력은 AI 연구 및 개발에서 필수적인 요소가 될 것입니다. 🚀

2930 Blog에서 더 알아보기

구독을 신청하면 최신 게시물을 이메일로 받아볼 수 있습니다.